Diffrazion

Quest articol chì l'è scrivuu in lombard, grafia milanesa.

La diffrazión , in fisica, a l’è on fenòmen associàa con la deviazión del tragìtt de propagazion di ond quand che sti chì incontren ‘n’ostàcol adrée al sò passàa. A l’è tipica de qualsessìa géner de onda, compagn del son, di ond in su la superfice de l’acqua o i ond elettromagnetich compagn de la la lus oppùr i ond radio; el fenòmen el succed anca in di situazion particolar indoe la materia la gh’ha di proprietàa ondulatòri, segond el dualismo onda-particola.

I effètt de la diffrazión hinn rilevant quand che la longhèzza d’onda l’è paragonàbil con la grandèzza de l’ostàcol: in particolar per la lus visibel (longhèzza d’onda intorna de 0,5 µm) succeden di fenòmen de driffrazion quand che la lus l’interagìss con di oggètt de misura inferióra di millimeter.

Stòria

La definizion de "diffrazion" insci com’è che l’è in del trattàa del Francesco Maria Grimaldi.

Qualsessìa deviazion de on ragg de lus che la sia nò caosada de la riflession o de la rifrazion a l’è ciamada diffrazion. Quèsta chì a l’è la definizion classica trovada in del trattàa classich de Òttica del Arnold Sommerfeld^[1]. A l’è sorprendent de notà che quèsta definizion chì la ghe va adrée a quèll che l’è stàa descrivùu del Gesuita Francesco Maria Grimaldi (ved la definizion original ind la segonda figura che la riprodùss el paràgraf original in del trattàa del F. M. Grimaldi), che l’ha inventàa el tèrmen che ‘l voeur dì "división in divèrsi part" in del 1665^[2]. Isaac Newton l’hà taccàa adrée la caosa del fenòmen a ona piegadura di ragg sberlusent (senza osservà, compagn de tutt i òttich newtoniàn, i franz denter in de l’ombrìa de on cavèll)^[3].

El tèrmen newtoniàn che ‘l designa la diffrazion a l’è inflexion. El Thomas Young l’hà studiàa la diffrazion come ‘na sòma de la lus trasmisa direttament de là de n’avertùra (o d’on ostàcol) in su on schèrmo e on onda che la nàss de bòrd de l’avertùra o de l’ostàcol. El Augustin-Jean Fresnel l’hà doprà al princippi el modèll del Thomas Young, ma di sò esperiènz al fin de fa vedè i variazion de la figura de la diffrazion per mèzz di parametri caratteristich de bòrd (natura, geometria del bòrd) e ona inversadura rispètt a la posizion di franz scur ind la region de foeura de l’ombria de on cavèll preveduda, l’hànn indòtt a bandonà la teoria de l'onda de bòrdo (stabilida del A. Fresnel d’ona manera del tutt indipendenta del Thomas Young), a a’ndàgh inveci adrée a la teoria fondada sul princippio de l'Huygens, per mèzz de la quàl l’è riessì soratutt a fornì ona decrizion de fenòmen de pont de vista matematich.

A l’è de vèss notà che la teorìa de l'onda di bòrd del Thomas Young la gh’ha di precursór "Newtoniàn" vegnù innanz del Thomas Young, che la sò teorìa a l’è in on quàj ponto minga ciàra e senza priva di sostegn matematich. In gener la posizion del Thomas Young, ch’ a ghe se attribuìss el mérit de vèss stàa el primm a stabilì la natura periòdica de la lus, a l’è in realtàa minga cèrta (el tèrmen "longhèzza d'onda" a l’è mai stàa dopràa) inveci a l’è ona costanta di sò ricèrch l’analogia infra el "son" e "lus". Tuttamanch, ai temp di pionièr (T. Young e A. Fresnel) né la teoria de l'onda de bòrdo, né el princippi de l’Huygens gh’hann on sustègn teòrich^[4]^[5] che ‘l rivarà domà in del 1883 grazie al laorà del G. Kirchhoff^[6] e, anca se minga osservàa, del G. A. Maggi^[7] ind el 1886 per la teoria de l'onda de bòrd.

Generalitàa

Caratteristich qualitatìv de la diffrazion

Denanz de on fenòmen de diffrazion, in del caso òttico, se pòden fàa di osservazion preliminàr. El caso generàl del fenòmen a l’è la diffrazion del Fresnel (o da camp visìn), indoe la sorgent de lus e ‘l pian de osservazion hinn piazzàa a ona distanza finida de la filidura. La diffrazion del Fraunhofer (o de camp lontàn), inveci, a l’è on caso particolar de quèlla del Fresnel, ma assosènn pussée sempliz de vèss analizzada: defàtt quèsta chì la succéd quand che la sorgent e l’ pian hinn piazzàa a ‘na distanza infinida de la filidura, inscì che i ragg incidènt pòden vèss considerà parallel infra de lor. On esèmpi de quèll caso chì a l’è quèll d’ona sorgent de lus pontiforma (o dispòsta ‘m ‘na lìnea drizza), compagn del tràtt drizz del fil de ‘na lampadìnna o d’on fass laser vedùu d’ona distanza de dò par de meter travèrs dò lamètt distant infra de lor on mèzz décimm de millimeter. I caratteristich de la diffrazion hinn donca che:

la larghèzza del màssim centràl de la figura de diffrazion d’ona sola sfendidura a l’è el doppi di franz de fianch.
la larghèzza a l’è proporzional al’incontrari de la larghèzza de la sfendidura: a di filidùr molto piscinìnn corisponden franz de diffrazion molto largh e viceversa.
i angol di franz dipenden nò de la scala de l’esperiment, ma domà del rappòrt tra la longhèzza d’onda e la laghèzza de la filidura.
in qualsessìa fenòmen del Fresnel, on ostico che ‘l gh’abìa simmitria el gh’ha semper de la lus al center de l'ombrìa (a l’è el caso tipich de la "macchia di Poisson").

Esempi de diffrazion

Di fenòmen de diffrazion pòden vèss notà tucc i dì, in particolar quèj ch’interèssen la lus visìbel: per esempi, i tracc incìs in su la superfice de on CD o de on DVD fànn el mestèe d’ona graticola de diffrazion, e créen l’effètt conossùu de l’arcobalen; anca i olograma piscinìtt, ad esempi quèj di cart de credit, gh’hànn el sò fondament in del fenòmen de la diffrazion. In natura, a se pòden notà i color cangiant caosàa di diffrazion che se fànn interferenza vuna l’altra, compagn de quèj di piùmm del pavon, oppùr de la coràzza d’on quaj alcuni coleotter, o di al de tanti parpàI (figura a sinistra), ch’hinn coloràa grazie a l’interferenza di ond che subissen diffrazion effettuada de scaj microscòpich dispòst in dona manera regolà.

La diffrazion atmosferega caosada de gott d’acqua microscòpich in sospension l’è la responsabil di anèj de lus visìbel intorna di sorgent de lus (‘me i glòri); l’ombria de on oggètt, ancasì la po’ ‘vègh di fenòmen debol de diffrazion in sui bòrd. ‘Na figura che la gh’ha pussée de color compagna del parpai ind la fòto se osserva infra i fil del tessùu de n’ombrella quand che se varda ona lus lontana travèrs. La diffrazion a l’è on lìmit fisich per la rispòsta de qualsessìa istrument òttich e per quèst la riguarda divèrsi tecnologij, de già che, defàtt, la gh’impònn on lìmit a la risoluzion di macchin fotografegh, di cinepres, di telescòpi e di microscòpi.

Per via de la diffrazion i ond marin foeurmen di figur complicàd quand che incrusen on ostacol piscinìnn, compagn d’on faro in mar, o intravèrsen on’avertura strèccia (figura a drizza), ‘me ‘n canà o l’entrada de on pòrt.

Spiegazion del fenòmen

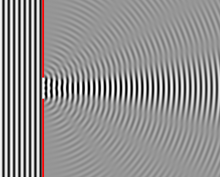
La diffrazion pò vegnì per intuit "leggiuda" ‘me ‘na domanda de continuità del front d’onda che ‘l subìss ‘na discontinuità per via del bòrd ( o di bòrd) d’on ostàcol. La figura de fianch, che la simula la diffrazion d’on’onda piana travèrs la sfendidura, la regorda quèll se nòta quand che on’onda in su la superfice de l’acqua la passa travèrs la fendidura. De là de la sfendidura el front d’onda incident a l’è "tajà" per mèzz de du bòrd. La parte del front d'onda arenta a ògni bòrd la piega intorna del bòrd medèsimm e ‘l fornìss inscì ona perturbazion continua. Second la ciav de lettura de la teoria de l'onda del bòrd a l’è ‘me se l’ostàcol el diventàss ona sorgent (immaginaria) d’on’onda de simmitria cilindrica de vèssegh sommada sia a l'onda trasmèssa second i leg de l'òttica geometrica e, ovviament, a l'altra onda de bòrd. Second la ciav de lettura del princippi de l'Huygens, el fronte d'onda incidenta a l’è l'invilupp di ond sferich elementàr. Chichinscì, i sorgent (immaginari) de quèj ond chì hinn in di pont denter ind la sfendidura. L'invilùpp de quèj ond sferich chì arent al bòrd el se propaga originand di noeuv front d’onda vun adrèe a l’alter. Amalastant la diferenza ind la descrizion del fenòmen, sia el modèll de l’onda del bòrd che ‘l modèll fondà in sul princippi de l’Huygens hinn a la fin de la fèra l’istèss de già che la "matematizzazion" de la teoria de l'onda del bòrd la ven de la matematizzazion de la teoria de la propagazion second el princippi de l’Huygens. Vii a vedè per quèst i riferiment [6] e [7] del la sezione storica precedenta.

Descrizion matematica de la diffrazion

Per capì i effètt de la diffrazion se gh’hà primma de tutt de trovà la fase e l’intensità d’ògni sorgent de l’Huygens in tucc i pont de spazzi; quèst el voeur dì ch’a se dev calcolà per ògni pont la soa distanza del front d’onda: se la distanza de ògni pont l’è divèrsa a men de on numer intrègh de longhèzz d’onda, tucc i sorgen hinn in fase e originerànn on’interferenza che se sommen; se al’incontrari la distanza l’è divèrsa per via de on numeri intrégh pussée mèzza longhèzza d’onda, originerànn on’interferenza che se destrugghen. Generalment capì i posizion de quèj massìm e minìmm chì a l’è assée de ottegnì ona descrizion complètta de fenòmen.

La descrizion pussèe sempliz de diffrazion a l’è quèlla del caso de on problema in du dimension, comepagn che ‘l caso di ond de l’acqua che se propaghen domà in su la superfice del liquid; inveci per el caso di ragg sberlusent, a se pò trascurà ona di trè misur de la sfendidura domà se l’è molto pussée granda de la longhèzza d’onda de la lus; in del caso di sfendidor circolar, inveci, se gh’hà de considerà tutt e trè i misur.

Analisi quantitativa de la diffrazion d’ona ùnega sfendidura

Grafich e immagin de la diffrazion d’ona ùnega sfendidura

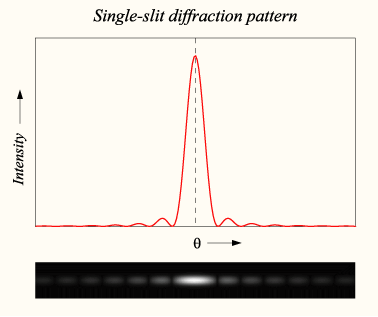
‘Me esempi, a se pò recavà on’equazion pussée precisa che la liga insèma l’intensità di band de diffrazion con l’angol al qual se consideren, in del caso de ‘n’ùnega sfendidura: per partì con la rappresentazion matematica del princippi de l'Huygens se considera on'onda monocromatica $\Psi ^{\prime }$ de longhèzza d'onda λ incidenta in su ‘na sfenditura de ampièzza a in sul pian complèss; se quèsta sfendidura chì l’è mìsa in sul piàn definì per mèzz di ass x′-y′ (con center ind l’origin), se pò ipotizzàa che la diffrazion l’ingeneri on'onda complèssa $\Psi$ che la viaggia adrée a la direzion radiàl r rispètt a la sfendidura che la soa equazion a l’è:

\Psi =\int _{fend.}{\frac {i}{r\lambda }}\Psi ^{\prime }e^{-ikr}\,df

Considerèmm adéss (x′,y′,0) on pont dent ind la sfenditura: se (x,0,z) hinn i coordinàd indoe gh’è de misurà l'intensità de la figura de diffrazion, la sfenditura la se spantegarà de $x^{\prime }=-a/2$ a $x^{\prime }=+a/2$ segond on vèrso e da $y'=-\infty$ a $y'=+\infty$ segond l’alter.

La distanza r da la fenditura l’è:

r={\sqrt {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}+z^{2}}}

r=z\left(1+{\frac {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}}{z^{2}}}\right)^{\frac {1}{2}}

Cont el considerà el caso de la diffrazion del Fraunhofer, el risultarà che:

z\gg {\big |}\left(x-x^{\prime }\right){\big |}

In alter paròll, la distanza del schèrmo a l’è assosènn pussée granda de l'ampièzza de la fenditura; con l'ajut del teorema binomial, ghe se pò tirà visìn a quèsta distanza chi inscì:

r\approx z\left(1+{\frac {1}{2}}{\frac {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}}{z^{2}}}\right)

r\approx z+{\frac {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}}{2z}}

Mettendo quèll valór chi de r ind la prima equazione se troeuva:

$\Psi$	$={\frac {i\Psi ^{\prime }}{z\lambda }}\int _{-{\frac {a}{2}}}^{\frac {a}{2}}\int _{-\infty }^{\infty }e^{-ik\left[z+{\frac {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}}{2z}}\right]}\,dx^{\prime }\,dy^{\prime }$
	$={\frac {i\Psi ^{\prime }}{z\lambda }}e^{-ikz}\int _{-{\frac {a}{2}}}^{\frac {a}{2}}e^{-ik\left[{\frac {\left(x-x^{\prime }\right)^{2}}{2z}}\right]}\,dx^{\prime }\int _{-\infty }^{\infty }e^{-ik\left[{\frac {y^{\prime 2}}{2z}}\right]}\,dy^{\prime }$
	$=\Psi ^{\prime }{\sqrt {\frac {i}{z\lambda }}}e^{\frac {-ikx^{2}}{2z}}\int _{-{\frac {a}{2}}}^{\frac {a}{2}}e^{\frac {ikxx^{\prime }}{z}}e^{\frac {-ikx^{\prime 2}}{2z}}\,dx^{\prime }$

Al fin de semplificà se pòden catà su i tèrmen costant e ciamàj C (el C el po’ ‘vègh denter di numer immaginari, anca se a la fin ψ el se podarà semplificà con el trà via sti component chì). Adèss, ind la diffrazion del Fraunhofer $kx^{\prime 2}/z$ a l’è assosènn piscinìtt, de manera de podè scriv $e^{\frac {-ikx^{\prime 2}}{2z}}\approx 1$ . Donca, de già che $C=\Psi ^{\prime }{\sqrt {\frac {i}{z\lambda }}}$ , el risultarà:

$\Psi \,$	$=C\int _{-{\frac {a}{2}}}^{\frac {a}{2}}e^{\frac {ikxx^{\prime }}{z}}\,dx^{\prime }$
	$=C{\frac {\left(e^{\frac {ikax}{2z}}-e^{\frac {-ikax}{2z}}\right)}{\frac {ikx}{z}}}$

Se pò notà con l'ajut de la formola de l’Eulero che $\sin x={\frac {e^{ix}-e^{-ix}}{2i}}$ e $\sin \theta ={\frac {x}{z}}$ :

$\Psi =aC{\frac {\sin {\frac {ka\sin \theta }{2}}}{\frac {ka\sin \theta }{2}}}=aC\left[\operatorname {sinc} \left({\frac {ka\sin \theta }{2}}\right)\right]$

Cont l’impònn: $\operatorname {sinc} (x)\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\operatorname {sin} (x)}{x}}$ .

Infina, cont el mètt denter in ${\frac {2\pi }{\lambda }}=k$ , l'intensità $I$ di ond che subissen diffrazion a on dàa angol a l’è dada de:

I(\theta )\,

=I_{0}{\left[\operatorname {sinc} \left({\frac {\pi a}{\lambda }}\sin \theta \right)\right]}^{2}

Analisi quantitativa de la diffrazion fada de N sfendidur

Diffrazion de ‘na doppia sfendidùra de ‘n ragg laser.

Considerèmm de noeuv el princippi de l'Huygens

\Psi =\int _{fend.}{\frac {i}{r\lambda }}\Psi ^{\prime }e^{-ikr}\,dfend.

Adèss se consideren N sfendidùr de l’istèssa ampièzza (a, $\infty$ , 0) distant vuna de l’altra de ‘na longhèzza d adrée a l’ass x′. Come l’è stàa tràa foeura primma, la distanza r da la primma sfendidura la sarà:

r=z\left(1+{\frac {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}}{z^{2}}}\right)^{\frac {1}{2}}

Per considerà anca el casò de N sfendidùr, a se pò innanz de tutt notà che intanta che z e y rèsten costànt, x′ la varia in quèsta manera chì:

x_{j=0\cdots n-1}^{\prime }=x_{0}^{\prime }-jd

Donca s’ottén che:

r_{j}=z\left(1+{\frac {\left(x-x^{\prime }-jd\right)^{2}+y^{\prime 2}}{z^{2}}}\right)^{\frac {1}{2}}

e la sòma de tucc i N contribuzion a l'onda l’è:

\Psi =\sum _{j=0}^{N-1}C\int _{-{\frac {a}{2}}}^{\frac {a}{2}}e^{\frac {ikx\left(x^{\prime }-jd\right)}{z}}e^{\frac {-ik\left(x^{\prime }-jd\right)^{2}}{2z}}\,dx^{\prime }

A se pò notà ancamò che ${\frac {k\left(x^{\prime }-jd\right)^{2}}{z}}$ a l’è trascurabil, de manera che $e^{\frac {-ik\left(x^{\prime }-jd\right)^{2}}{2z}}\approx 1$ ; donca el risulta:

$\Psi \,$	$=C\sum _{j=0}^{N-1}\int _{-{\frac {a}{2}}}^{\frac {a}{2}}e^{\frac {ikx\left(x^{\prime }-jd\right)}{z}}\,dx^{\prime }$
	$=C\sum _{j=0}^{N-1}{\frac {\left(e^{{\frac {ikax}{2z}}-{\frac {ijkxd}{z}}}-e^{{\frac {-ikax}{2z}}-{\frac {ijkxd}{z}}}\right)}{\frac {2ikax}{2z}}}$
	$=C\sum _{j=0}^{N-1}e^{\frac {ijkxd}{z}}{\frac {\left(e^{\frac {ikax}{2z}}-e^{\frac {-ikax}{2z}}\right)}{\frac {2ikax}{2z}}}$
	$=C{\frac {\sin {\frac {ka\sin \theta }{2}}}{\frac {ka\sin \theta }{2}}}\sum _{j=1}^{N-1}e^{ijkd\sin \theta }$

Adèss a se pò doprà quèlla eguaglianza chichinscì:

$\sum _{j=0}^{N-1}e^{xj}={\frac {1-e^{Nx}}{1-e^{x}}}.$

de mètt dent ind l’equazion e inscì ottegnì:

$\Psi \,$	$=C{\frac {\sin {\frac {ka\sin \theta }{2}}}{\frac {ka\sin \theta }{2}}}\left({\frac {1-e^{iNkd\sin \theta }}{1-e^{ikd\sin \theta }}}\right)$
	$=C{\frac {\sin {\frac {ka\sin \theta }{2}}}{\frac {ka\sin \theta }{2}}}\left({\frac {e^{-iNkd{\frac {\sin \theta }{2}}}-e^{iNkd{\frac {\sin \theta }{2}}}}{e^{-ikd{\frac {\sin \theta }{2}}}-e^{ikd{\frac {\sin \theta }{2}}}}}\right)\left({\frac {e^{iNkd{\frac {\sin \theta }{2}}}}{e^{ikd{\frac {\sin \theta }{2}}}}}\right)$
	$=C{\frac {\sin {\frac {ka\sin \theta }{2}}}{\frac {ka\sin \theta }{2}}}{\frac {\frac {e^{-iNkd{\frac {\sin \theta }{2}}}-e^{iNkd{\frac {\sin \theta }{2}}}}{2i}}{\frac {e^{-ikd{\frac {\sin \theta }{2}}}-e^{ikd{\frac {\sin \theta }{2}}}}{2i}}}\left(e^{i(N-1)kd{\frac {\sin \theta }{2}}}\right)$
	$=C{\frac {\sin \left({\frac {ka\sin \theta }{2}}\right)}{\frac {ka\sin \theta }{2}}}{\frac {\sin \left({\frac {Nkd\sin \theta }{2}}\right)}{\sin \left({\frac {kd\sin \theta }{2}}\right)}}e^{i\left(N-1\right)kd{\frac {\sin \theta }{2}}}$

Ancamò, sostituìssom k e introdùssom la variàbil $I_{0}$ al pòst di costant minga oscillant, ‘me ind la diffrazion de ‘na sfendidura, de manera de semplicà el risultàa; regordandoss che:

\langle e^{ix}{\Big |}e^{ix}\rangle \ =e^{0}=1

se pòden trà via i espopnenziaj e ottegnì:

I\left(\theta \right)=I_{0}\left[\operatorname {sinc} \left({\frac {\pi a}{\lambda }}\sin \theta \right)\right]^{2}\cdot \left[{\frac {\sin \left({\frac {N\pi d}{\lambda }}\sin \theta \right)}{\sin \left({\frac {\pi d}{\lambda }}\sin \theta \right)}}\right]^{2}

Diffrazion de 'n'avertura circolar

Per savenn pussee, varda l'articol Disco de l’Airy.

On *disco de l’Airy* fàa su per mèzz de on modèll al compiuter.

La diffrazion d’on'onda piana incidenta in su ‘n'avetùra circolar la fornìss ‘me risultàa l’inscì ciamà disco de l'Airy. La variazion de l'intensità de l'onda in funzion de l'angol a l’è dada de l'espression:

I(\theta )=I_{0}\left({\frac {2J_{1}(ka\sin \theta )}{ka\sin \theta }}\right)^{2}

indoe a a l’è el ragg de l'avertura, k a l’è pari a 2π/λ e J₁ a l’è ‘na funzion del Bessel. Se l’avertura a l’è pussèe piscinina, la sarà pussée granda la dispersion di ond, a lassà fissa la distanza.

Alter casi de diffrazion

Lìmit de diffrazion per i telescòpi

El disco de l'Airy intorna d’ogni stèlla el pò vèss osservà con on telescòpi de 2.56 meter de avertura ind l’imagin chichinscì del sistéma binari del Zeta Boötis.

In del caso de la diffrazion de ‘n'avertura circolar, a se releva ona serie de anèj concentrich intorna del disco de l'Airy. L'analisi matematica de quèst specifich caso a l’è compagna de la version doprada per la diffrazion de ‘n’ùnega sfendidura vista prìmma.

On'onda al fin de subì ‘na diffrazion la gh’ha nò per fòrza besògn d’intreversà ona sfenditura: per esempi, anca on ragg de lus de ampièzza finida el subiss on procèss de diffrazion e l’aumenta la soa ampièzza. Quèll fenòmen chì el limita l'ampiezza d di apparècc indoe la se concentra la lus, in del foeugh d’ona lenta; chesschì a l’è conossùu ‘me lìmit de diffrazion:

d=1.22\lambda {\frac {f}{a}},\,

indoe λ a l’è la longhèzza d'onda de la lus, f a l’è la distanza focal de la lenta e a l’è el diametro del ragg de lus o (se ‘l ragg de lus a l’è pussé ampi de la lenta el diametro de la lenta. L'ampièzza che la risulta la gh’ha dent circa el 70% de l'energia de la lus e la corrispond al ragg del primm mìnim del disco de l'Airy, calcolà de manera de tiràss visìn con el criteri del Rayleigh; el diametro del prim mìnimm, che ‘l gh’hà dent l'83.8% de l'energia de la lus, a l’è despèss doprà ‘me "diametro de diffrazion".

Con l’uso del princippi de l'Huygens, la ven trà foeura la superfice de diffrazion d’on’onda che l’intravèrsa ‘na sfendidura de qualssessìa forma: se quèsta superfice chì la ven osservada a na cèrta distanza de l'avertura, la sarà la trasformada del Fourier in dò misur de la funzion che la rappresenta l'avertura.

Diffrazion del Bragg

Per savenn pussee, varda l'articol Leg del Bragg.

La diffrazion de tanti sfendidùr descrivuda primma a l’è on fenòmen compagn de quèll che ‘l succed quand che on’onda la ven mandada in gir de ‘na struttura periòdica, ‘me la graticola de atomi de on cristàll o i grat de ona graticola de diffrazion. Ògni pont de diffusion, per esempi ògni atom del cristàll, l’agiss ‘me ona sorgent pontiforma de ond sferich, che originerànn di fenòmen de interferenza che i ond se sòmen a fa su on cèrt numer de ond diffràtt. La direzion sti ond chì a l’è descritta de la Leg del Bragg:

m\lambda =2d\sin \theta \

indoe λ a l’è la longhezza d'onda, d a l’è la distanza intra ògni pont de diffusion, θ l’è l'angolo de diffrazione e m a l’è on numero intrègh che l’indica l'ordin de ògni onda diffratta. La diffrazion del Bragg la ven doprada ind la cristallografia a ragg X de trà foeura la struttura d’on qualsessìa cristall per via de l’analisi di angol che i raggi X subissen diffrazion del cristall medèmm: de già che l’angol θ de diffrazion el dipend de la longhezza d'onda λ, ona graticola de diffrazion la càosa ona dispersión angolar d’on ragg de lus.

L'esempi pussée sempliz de diffrazion del Bragg a l’è el spèttro di color che ‘l se pò vedè riflettùd de on CD: la distanza piscinina infra i tracc in su la superfice del disco la fa su ona graticola de diffrazion e ciascheduna di component de la lus bianca la subìss diffrazion con di angol divèrsi, segond la legg del Bragg.

Diffrazion di partìcol

Per savenn pussee, varda i articoi Diffrazion de l'elettron e Diffrazion del neutron.

La diffrazion de partìcol elementar ‘me i elettron l’è vuna infrà i ròbb pussée important de la meccanica quantistica: l’osservazion de la diffrazion d’on elettron o d’on neutron la fa vedè l’esistenza del dualismo onda-partìcola; quèsta diffrazion chi a l’è anca on instrument scientifich che ‘l pò servì: la longhèzza d'onda de sti partìcol chì a l’è assée piscinina de vèss doprada per la scansion de la struttura atòmica di cristàj.

La longhèzza d'onda associada a ‘na partìcola a l’è inscì ciamada longhezza d'onda del De Broglie:

\lambda ={\frac {h}{mv}}

indoe h a l’è la costanta del Planck e v e m hinn vuna la velocità e l’altra la massa de la partìcola; λ a l’è caratteristica de qualsessìa oggètt materiàl, anca se la po’ vèss relevada domà per i oggètt piscinìtt piscinìtt, compagn di atom e d’alter partìcol.

De recent, a l’è stada osservada la diffrazion di partìcol ciamàa barion e de on particolar tipo de fullerene chiamato buckmisterfullerene; el fin de la ricerca che la vegnerà el sarà quèll de osservà la diffrazion di virus, che, de già che gh’hànn molta pussée de massa di partìcol elementar, gh’hann ona longhèzza d'onda inferioria, insci che gh’hànn de intraversà adasi adasi ona sfendidura molto suttil de manifestà i caratter di ond.

Financa la Terra la gh’ha ona soa longhezza d'onda (in realtàa, on qualsessìa oggètt che ‘l gh’abia ona quantità de moto la gh’hà): de già che la gh’ha ‘na massa de circa 6×10²⁴ kg e ‘na velocità orbital media de circa 30000 ms⁻¹, la gh’ha ‘na longhezza d'onda del De Broglie pari a 3.68×10⁻⁶³ m.

La coerenza

Per savenn pussee, varda l'articol Coerenza (fisica).

La descrizion de la diffrazion l’è fondada, ‘me ditt prima, in su la descrizion de l'interferenza intra di ond generàa de l’istèssa sorgent (e che donca pàrten de l’istèss sit) ma che vànn adrèe a direzion divèrsi; in quèll modèll chì, la differenza de fase intra i ond la dipend domà de la longhèzza effettiva del tragìtt; el pò succed però che dò ond emìss in di moment divèrsi de la sorgent riven in sul schèrmo in du pont divèrsi ma in del’istèss moment; la fase inizial con la qual la sorgent l’ingenera i ond la pò anca cambià in del cors del temp: i ond emèss infra di intervàj de temp assée longh sarànn nò bon de formà ona figura de interferenza stabil, perché la sò differenza de fas la sarà pù indipendenta del temp.

La longhèzza correlada con la fase d’on'onda elèttromagnetica ‘me la lus a l’è ciamda longhèzza de coerenza: al fin che la succeda ona interferenza, la differenza di tragìtt de dò ond la gh’hà de vèss pussée piscinina de la longhèzza de coerenza.

Se i ond hinn mandà foeura de ona sorgent estesa, quèst el pò prodù on’incorerenza adrèe a la direzion trasversàl: se se osserva de perpendicolar on ragg de lus, la longhèzza per la qual i fasi hinn correlàd a l’è ciamda longhèzza de coerenza trasversàl; in del caso de la diffrazion de la sfendidura doppia, el fenòme de la diffrazion el succederà domà se la longhèzza de coerenza traversàl a l’è inferiora de la distanza tra i do avertùr.

In del caso de la diffrazion de partìcol, la longhèzza de coerenza a l’è ligad con l'estension in del spazzi de la funzion d'onda che la descriv quèj partìcol là.

Riferiment

↑ A. Sommerfeld, Optics (Academic press, New York, 1954) p.179.
↑ Physico-mathesis de lumine, coloribus et iride (Bonomiae, 1665).
↑ I. Newton, Opticks, (London, 1704) Book 3.
↑ G. N. Cantor, "Was Thomas Young a wave theorist?", Am. J. Phys. 52, 305 - 308 (1984).
↑ S. Ganci, "Historical notes on the first viewpoint about light diffraction", Quaderni di Storia della Fisica, 13, 59 - 65 (2005).
↑ G. Kirchhoff, "Zur Theorie der Lichtstrahlen", Wied. Ann. 18, 663 - 695 (1883).
↑ G. A. Maggi, "Sulla Propagazione Libera e Perturbata delle Onde Luminose in um Mezzo Isotropo", Ann. Matematica, 16, 21 - 47 (1888).

Vos correlaa

Ligamm de foeura

(EN) Wave Optics
(EN) 2-D wave java applet mostra le bande di diffrazione che si formano utilizzando diverse configurazioni di fenditure.
(EN) Diffraction java applet mostra bande di diffrazione per fenditure di vari forme.
(EN) Diffraction approximations illustrated sito del MIT che illustra le varie approssimazioni utilizzate nello studio della diffrazione.
(EN) Diffraction Limited Photography spiega come i vari fenomeni di diffrazione limitino la risoluzione di ogni tipo di apparecchio ottico.
(EN) Diffraction and acoustics.
(EN) Gap Obstacle Corner - Simulazioni Java della diffrazione delle onde del mare.
(EN) Google Maps - Suggestiva immagine satellitare della diffrazione delle onde dell'oceano che entrano nel Canale di Panama.

[1] A. Sommerfeld, Optics (Academic press, New York, 1954) p.179.

[2] Physico-mathesis de lumine, coloribus et iride (Bonomiae, 1665).

[3] I. Newton, Opticks, (London, 1704) Book 3.

[4] G. N. Cantor, "Was Thomas Young a wave theorist?", Am. J. Phys. 52, 305 - 308 (1984).

[5] S. Ganci, "Historical notes on the first viewpoint about light diffraction", Quaderni di Storia della Fisica, 13, 59 - 65 (2005).

[6] G. Kirchhoff, "Zur Theorie der Lichtstrahlen", Wied. Ann. 18, 663 - 695 (1883).

[7] G. A. Maggi, "Sulla Propagazione Libera e Perturbata delle Onde Luminose in um Mezzo Isotropo", Ann. Matematica, 16, 21 - 47 (1888).

[1]

[2]

[3]

[4]

[5]

[6]

[7]