Vetor (fisega)
| Quell articol qì l'è scrivud in Lombard, cond l'ortografia Scriver Lombard. |
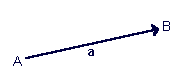
In fisega un vetor l'è un concet matemateg e un segment orientad qe sa dovra per descriver i grandeze come la velocitaa, l'acelerazion o la forza, ind i quale l'è important considerar mìa doma 'l valor ma anc la direzion e 'l vers. Al se representa cond un segment orientad per far veder ol so vers, ol so modul (la lungeza de la fliça) e 'l pont d'aplicazion.
Proprietaa
[Modifega | modifica 'l sorgent]I vetor s'pœl representar con di letere, cond una fliça sora, insé: .
Un vetor 'l g'ha qeste proprietaa qé:
- Pont d'aplicazion, l'è l'orijen del segment.
- Modul, esprimid dal valor numerig de la grandeza vetoriala. Al sa representa con la lungeza del segment, semper in valor assolut. Per esempe, se s'vœl dir qe 'l modul de al val 5 unitaa, se fa insé: .
- Direzion, qe l'è qella del segment. A la reta qe la g'ha dent ol vetor l'è ciamada linia d'azion.
- Vers, al far distinzion intra do vetor sœ la stessa linia d'azion.
Se dix qe do vetor i è concorrents quand qe i g'ha l'istess pont d'aplicazion.
Un vetor opost a un olter l'è qell qe 'l g'ha l'istess pont d'aplicazion, modul e direzion ma vers contrare. Insé 'l vetor opost a l'è .
In formule, dait un vetor de coordenade (x,y,z) ) ol so modul l'è . La so direzion l'è daita da la reta qe la g'ha dent ol vetor e 'l vers al pœl vesser d'una o de l'oltra banda.
S'pœl anc separar ol modul e dar la direzion e 'l vers a un vetor unitare qe l'è calcolad insé: , con i,j,k i vetor (1,0,0), (0,1,0) e (0,0,1) rispetivament.
Soma e sotrazion di vetor
[Modifega | modifica 'l sorgent]Metodo grafeg
[Modifega | modifica 'l sorgent]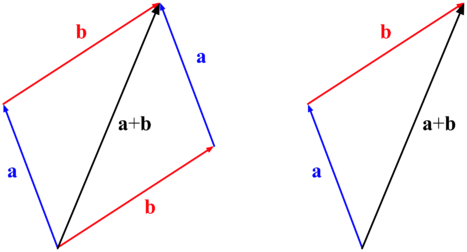
Per la soma e la sotrazion di vetor g'è de tegn in cunt, olter qe a la grandeza scalare, la direzion e 'l vers del vetor.
Metodo analiteg
[Modifega | modifica 'l sorgent]Modul resultant
[Modifega | modifica 'l sorgent]Daits do vetor e , de modui cognossids e qe formen l'angol intra de lor, s'pœl calcolar 'l modul insé:
Otegnir la direzion
[Modifega | modifica 'l sorgent]Per otegnir i angoi diretor a 'm g'ha de cognosser l'angol e de hir-ga jamò calcolad .
A 'm pœl dovrar qesta formula:
Con qesta m'ha otegnid ol sinus, e per trovar i angoi a partir del sinus a 'm g'ha de regordar-s qe:
Angol intra do vetor
[Modifega | modifica 'l sorgent]Per calcolar l'angol intra do vetor sa dovra qesta formula:
L'è possibel jeneralizar a qualsvœl dimension:
Quand a 'm lavora in manera aljebrega ind un spaze vetorial l'angol intra do vetor l'è dait da:
Con <,> segnad ol prodot scalar definid ind el istess spaze vetorial.

















