Nümar àuri
| Artícuj relazziunaa a Matemàtica |
| Quest articol chi l'è scrivuu in Koiné occidentala. |
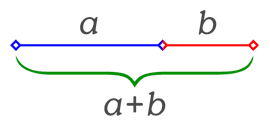
La resú àuria, sezziú àuria u divina prupurziú al è la relazziú intra düü segmeent a e b (u par estensiú, chela intra dò quantitaa a e b) si intra ul total e ul segmeent magjuur a gh’è la istessa relazziú che intra ul segmeent magjuur e ul segmeent minuur, u, in d’otre parole, si ul tütt al è al segmeent magjuur istess che ul magjuur al è al segmeent minuur. Cjamaant a ul segmeent (u nümar) magjuur e b ul minuur, la furmulazziú matemàtega da la definizziú sa la pöö scriif cuma:
Ul quozzieent da cheste dò quantitaa al resülta vess un nümar irazziunaal cugnussüü cuma nümar auri u nümar d'òor, e designaa abitüalameent par la lètera grega Φ (fi majüscula) in unuur al Fídia, scültuur e architett greech dal Partenú:
Le furme definide cun la resú àuria i è stade fisc da spess cunsiderade estéticameent agradàbile in la cültüra d'ucideent, da manera che la prupurziú divina al è stada duvrada da frequeent luungh la Stòria in l'aart e íntal disegn. Uviameent, apó al è staa duvrada la inversa da la resú àuria, da nurmaal representada par la lètera (fi minüscula) dal alfabett greech.
Però la resú àuria apó al è pussíbil la truvá in la natüra. Ul nümar d'òor al gh’a da plüü un bell puu da prupietaa cüriuse e interessante che i a faa inscí che la resú àuria l’àbies diventaa fascinanta par un bell puu da stüdiuus.
Definizziú e prime prupietaa dal nümar d'òor[Modifega | modifica 'l sorgent]
Cuma al è staa definii in l'incapsülameent, dò quantitaa a e b (cun a > b) i è in resú àuria si la suva suma al è a la quantitaa magjuur istess che la magjuur al è a la quantitaa minuur, i.e.:
Da manera equivaleent (par vidé l'equivalenza noma al cuventa mültiplicá in cruus e reurdená), dò quantitaa a e b i è in resú àuria si intra la magjuur e la menuur a gh’è la istessa prupurziú che intra la menuur e la suva diferenza, i.e.:
Da la prima equazziú (u apó da la segunda), uperaant sa riva a la seguenta equazziú: , d'indúe sa l uteegn:
indúe la darera igualtaa s'efetua traant fö fatuur cumü da b. Finalameent, si sa dividiss a banda e banda par b (che al è mia nüll), s'i uteegn le dò seguente valuur par :
Ul nümar d'òor al è noma la valuur positiva gja che al gh’a mia sentüü da parlá d'una quantitaa negativa par la resú intra düü segmeent.
Le prime prupietaa dal nümar d'òor i è dò:
- Ul nümar d'òor al è l'ünich reaal pusitiif che al è esattameent una ünitaa par sota dal sò quadraa.
- Demustrazziú: Mültiplicaant la prima equazziú da chesta sezziú par a/b (u bé par (a-b)/b la segunda) sa l uteegn:
- , u bé, feent la süstituzziú
- , Q.E.D.
- Ul nümar d'òor al è l'ünich reaal pusitiif che al è una ünitaa par sura dal sò invers.
- Demustrazziú: Cuma che Φ al è difereent da zero, sa pöö dividí l'equazziú anteriuur par Φ, da manera che
- , Q.E.D.
Urígen[Modifega | modifica 'l sorgent]
Resú fisc pròssime a l'àuria s'i a truvaa in le pusizziú e prupurziú da le piràmide da Giza, inscí che al sembra vess che i primm a duvrá la resú àuria i è staa i andeegh egizzià. Al è mia inscí cjaar si i je duvrava cunscjameent par da le qualitaa estétiche da la resú u si la suva prima aparizziú al è früit d'otre resú u dal asaart.
In l’andega Grecja sa i cugnussea bé vargüne prupietaa geumétriche da la resú àuria, par la suva frequenta aparizziú in geumetría; epüür, al sembra mia ceert che i en pröves la valuur estética. Malgraa tütt, int un bell puu da munümeent, cuma íntal Partenú, sa al pöö ga truvarde le prupurziú divine u fisc pròssime a chela. Al è staa mia pruvaa che cheste relazziú i füdess espressameent cercade, però molta geent la creet che al pöö mia vess ünicameent una questiú d'asaart.
In l'architetüra rumana apó sa i pöö truvá resú àurie, però al è mia staa pruvaa che i füdess espressameent druvade int i diseegn.
Resú àurie in geumetría[Modifega | modifica 'l sorgent]
Sezziú àuria d'un segmeent[Modifega | modifica 'l sorgent]

Daa un segmeent AB, sa diis che ul puunt S al custitüiss sezziú àuria dal segmeent AB (u al dividiss da furma àuria) si la paart plüü granda al è média geumétrica intra ul segmeent AB e la paart petita. Si la part petita a l’è SB, cuma in la figüra, matemàticameent vargott sa al diis:
Da manera equivalenta vargott al passa cura ca ul segmeent intreegh al è a la part granda cuma la paart granda al è a la petita, e.e.
L'equivalenza intra le definizziú sa la veet par esempi mültiplicaant in cruus la segunda espressiú.
Apó sa la veet l'equivalenza intra cheste definizziú e chela da càpsüla: in efett, si AS al misüra a e SB al gh’a una misüra b (e alura AB al gh’a una misüra a + b) e tütt cheest-chí sa l süstituiss in la segunda espressiú, sa l uteegn
La sezziú àuria dal segmeent int una paart granda e una petita la gh’a da plüü la prupietaa seguenta:
- La part petita al è segmeent auri da la paart granda, e.e.
- u bé
- Demustrazziú: si (par vess AS ul segmeent auri da AB), restaant a banda e banda sa l uteegn che
- Traant fö i fatuur cumü, e tegniint in cüünt che
- .
- Alura, , Q.E.D.
- Demustrazziú: si (par vess AS ul segmeent auri da AB), restaant a banda e banda sa l uteegn che
Custrüzziú da resú àurie cun riga e cumpass[Modifega | modifica 'l sorgent]
- Divisiú àuria d'un segmeent daa. Una da le custrüzziú plüü sémplis al è la seguenta:
- Trazzée BC, perpendicülaar a AB par B e da lunghezza la metaa da AB.
- Cun céntar a C, traspurtée la distanza CB sura la iputenüsa CA. Sa l uteegn inscí ul puunt D.
- Cun céntar a A, traspurtée la distanza AD sura ul segmeent AB. La intersezziú da cheest aarch cul segmeent AB al definiss ul puunt S cercaa, ch’al custitüiss sezziú àuria d'AB.
- Custrüzziú dal segmeent taal che ul sò segmeent auri al è ul daa. Chesta al è una da le custrüzziú plüü famose cun la resú àuria:

- Trazzée SC, perpendicülaar a AS par S e da lunghezza iguala a AS.
- Truvée ul puunt medi M dal segmeent AS (par esempi cun la mediatriu).
- Cun céntar a M, trazzée l'aarch cun radi MC. La intersezziú B da cheest aarch cun la reta süpòort da AS la definiss ul segmeent cercaa AB, ul segmeent auri dal quaal al è AS.
Triàngul d'òor[Modifega | modifica 'l sorgent]
I triàngul d'òor i è chij triàngul isòscej i custaa di quaj i è in resú àuria. N'a gh’è da düü tiip: chij che , che i è acutàngul e i che , che i è utusàngul. Chiist darée da spess i è apó numenaa triàngul d'argeent, però i gh’a mia vargott a vidé cul nümar d'argeent (che al gh’a mia vargott a vidé cun φ, l'invers da Φ).

I triàngul d'òor i gh’a düü àngul da 72º e ü da 36º; i triàngul d'argeent i gh’a düü àngul da 36º e ü da 108º. Chiist i è i istess àngul ch’i pariss apó íntal Pentàgon regülaar e ul pentàcul, indúe al è mia surprendeent da retruvá i triàngul d'òor e la resú àuria.
- Demustrazziú: In la figüra da manzina, sa pöö vidé cuma ul triàngul ABD al è símil al triàngul BCA gja che i düü i è isòscej e i gh’a un àngul in cumü. Inscí, i àngul ABD e ACB i è iguaj. La resú da similitüda a l’è, par la custrüzziú di triàngul 1/&Phi. Alura, ul segmeent AD al misüra 1/Φ.
- Cuma che ul nümar d'òor al verifica la igualtaa
- ,
- ul segmeent DC misüra 1, da manera che ul triàngul BCD al è isòscel e i àngul DCB e DBC i è iguaj. Par taant, cuma che DCB e ACB i è iguaj, ABD e DBC i è iguaj e DB al marca la bisetriis dal àngul ABC. Cuma che la suma di àngul d'un triàngul la vaar 180°, le valuur di àngul al è da 36° paj plüü güzz (la quinta part d'un àngul plà) e da 72º paj plüü deerf, (dò quinte paart dal àngul plà u una quinta part d'un àngul cumplett).
Retàngul d'òor[Modifega | modifica 'l sorgent]

I retàngul d'òor i è chij retànguj i custaa di quaj i è in resú àuria.
La custrüzziú d'un retàngul d'òor cun cumpass sa la pöö fá fàcilmeent a partí d'un quadraa par la segunda custrüzziú chí-da-sura. Puntaant al céntar d'un di custaa e derveent fí a un di düü àngul upòost, noma al cuventa bassá l'aarch fí al prulungameent dal custaa indúe al è staa puntaa. Vöna da le prupietaa di retàngul d'òor al è che ul retàngul resültaant da l’eliminazziú dal quadraa da custaa b ch’al pöö generá (vidée la figüra), apó al è d'òor. Chesta prupietaa al è devüda al fatt che la resú àuria la cumpiss la prupietaa seguenta, gja vidüda in sezziú da prima:
- .
Ul pentàgon e ul pentalfa regülaar[Modifega | modifica 'l sorgent]

Ul Pentàgon regülaar e le suve diagunale, che i furma un pentalfa (u pentacle) i suunt un mücc da prupietaa relazziunade cun la resú àuria. Vargü i creet che cheest-chí al pudaress vess ü di mutiif paj quaj cheest símbul al è staa scernii par Pitàgura par la fradelanza che al creaa e presidea: i pitagòrich.
Par tratá-ss da Pentàgon regülaar, s'i identífega dees àngul da 108º, ciinch íntal Pentàgon esteriuur e ciinch plüü íntal interiuur. A partí da chiist dees àngul s'i en pöö truvá ciinch plüü apó da 108º (par àngul upòost pal vèrtes) e dees àngul da 72º (par àngul süplementari. Da chesta manera, s'i identífega ciinch triàngul d'òor, ch’i furma le punte dal pentàcul. Apó s'i identífega 15 triàngul d'argeent (da dò misüre diferente). Noma a gh’è dunca trii tiip d'àngul: da 36º, 72º (ul dobi da 36º) e 108º (ul trípel).

Pal ch’al fa a la lunghezza di segmeent, s'usserva che a ghe n è noma da quàtar lunghezze diferente, però tüte in relazziú àuria cun vargüna otra:
- Demustrazziú Par demustrá cadascüna da cheste relazziú, al cuventa noma truvá un triàngul d'òor u d'argeent furmaa par custaa cun le lunghezze curespundeent. I triàngul i è efetivameent d'òor u d'argeent par che l’i pröva i söö àngul e la relazziú a l’è àuria par definizziú da triàngul d'òor u d'argeent.
Spiraj d'òor[Modifega | modifica 'l sorgent]
Sa l pöö custruí, a partí d'una sequenza da retàngul d'òor e quadraa (vidée la figüra), una spirala trazzaant quaart da circumferenza in cada quadraa e tangeent a chel. Chesta spirala l’apròssima la'spirala d'òor, una spirala logarítmica da céntar la intersezziú da le dò diagunale indicade in la figüra e d'equazziú pulara:

Da la istessa manera, sa pöö custruí, a partí d'una sequenza da triàngul d'òor, una spirala aprussimada a la vertadera d'òor triangulara, apó spirala logarítmica però adess d'equazziú pulara:
Àngul d'òor[Modifega | modifica 'l sorgent]

Sa l nòmina àngul d'òor chel àngul utegnüü par la partizziú d'un círcül (la circumferenza dal quaal al gh’a una lunghezza c) in düü setuur circülaar, ul plüü graant cunt un aarch da lunghezza a e ul minuur, cunt un aarch da lunghezza b, da manera che
e preneent par bú l'àngul petit (ul da lunghezza d'aarch b).
Cuma che sa trata d'una partizziú dal círcul, apó sa al gh’a che , e par taant, (vidée ul paraleliism cun la sezziú àuria d'un segmeent).
- L'àngul d'òor al misüra , u bé in radiaant, .
- Demustrazziú: Da l’equazziú , uperaant sa riva a l'equazziú , d'indúe, resolveent, sa l uteegn:
- Da chí, s'i uteegn le do seguente valuur par :
- Cuma che taant a cuma b i è pusitiif, sa l gh’a che u che . Süstitueent in , e reurdenaant sa l uteegn che:
- , d'indúe sa la uteegn la misüra angulara dal àngul: u .
Ul nümar d'òor[Modifega | modifica 'l sorgent]
Prupietaa[Modifega | modifica 'l sorgent]
Gja che Φ al resülta da la sulüzziú d'una equazziú pulinòmica, al furma part dal cungjuunt di nümar algebràich. Al pöö vess demustraa apó che Φ al è un nümar irazziunaal.
- (vidée le prime 20000 scifre decimale dal nümar d'òor)
Vargüne espressiú cun le putenze da Φ:
Le putenze da Φ apó i cumpiss la seguenta prupietat:
- Demustrazziú: La prupietaa anteriuur sa la pöö utegní dal mültiplicá la igualtaa par .
- Inscí, le putenze natürale dal nümar d'òor i cumpiss la relazziú da recurenza da Fibonacci,
- Grazzia a chesta prupietaa, sa i pöö apó scriif espressiú indúe s'usserva la sequenza da Fibonaci:
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
Una otra prupietaa surprendenta relazziunada cun la recurenza da Fibonaci al è che ul quozzieent intra tèrmin cunsecütiif d'una sequenza definida cun chesta recurenza (intra cheste, la sequenza da Fibonaci) al teent al nümar d'òor. In efett, si a l’è una sequenza taal che , alura:
- Demustrazziú:
-
- Da , mültiplicaant par x, sa riva a:
- , una equazziú quadràtega gja cugnussüda cunt ariis e . La prima ariis a l’è la curespundeent a la part cresseent da la sequenza, Q.E.D. La segunda, al è la coresponeent a una iputética sequenza al indrée (cercaant ul límit .
Cuma che , sa pöö representá Φ in furma da frazziú cuntínua:
Cuma che , Φ sa pöö representá apó cunt una iterazziú infinida d'ariis quadrade:
Ul nümar d'òor al presenta apó prupietaa interessante si s'al dövra cuma basa d'un sistema da nümar (vidée basa d'òor).
In trigunumetría, ul nümar d'òor al è fisc relazziunaa cuj àngul ch’i pariss int un pentacle: (36º, 72º e 108º) e cun le suve metaa: 18º e 54º:
Ul nümar d'òor apó al paris in espressiú cuma
La resú àuria in le arte[Modifega | modifica 'l sorgent]

In 1509, Luca Pacioli al püblica Divina Proportione, indúe al tratava mia noma cun le cüriusitaa matemàteghe dal nümar d'òor, ma apó cul sò üüs in l'architetüra. Vargott al prupízzia l'acetazziú da la idea che un bell puu da artiist dal Renassimeent, ga i metess la resú àuria int i söö diseegn. Un bú esempi da chiist miit al è in le pitüre dal Leonardo Da Vinci, indúe, da la istessa manera che íntal Partenú, sa pöö truvar da le relazziú àurie, malgra ga síes mia da le pröve evidente ch’i cunfírmes che i füdess intrudüide espressameent pal istess autur.
Gja íntal sécul XIX, l’architett Svízzer Le Corbusier al püblica Le Modulor, indúe al tratava, intra d’òolt, cun la resú àuria in l’architetüra e suratütt in l’ürbaniism.
La resú àuria al a stada druvada in custrüzziú plüü recente cuma in scale, edifizzi e d’òolt, cuma par esempi in la misüra stàndard da carnet e carte da crédit ch’i s’apròssima a retàngul d’òor. Forsi l’edifizzi plüü emblemàtich al è la sò dal ONU a Növa York, un graant prisma cun vöna da le suve fasce in furma da retàngul d’òor.
La resú àuria apó al a stada druvada apó in müsica, tant par la dürada da le note (par esempi pal cumpusituur Ungarées Bela Bartok e ul francées Olivier Messiaen), cuma par l’urganizazziú da le parte d’un pezz (par esempi in vargüna övra dal cumpusituur Messicà Silvestre Revueltas) u apó in la relazziú intra le frequenze da növe note fö da la scala crumàtega (par esempi in For Ann (rising), da James Tenney).
A gh’è geent ch’a la creet che la resú àuria la gh’a prupietaa estétiche particülare. D’òolt i argümenta che qual-sa-vöör prupurziú cumpresa intra 1,4 e 1,8 en la gh’a.
Ul nümar d'òor in la natüra[Modifega | modifica 'l sorgent]
Resú aprussimadameent d’òor sa i pöö truvá in la ramificazziú da determinade piante u in la dispusizziú di pétal da le dàlie e otre fluur. Apó sa i pöö truvá spirale e àngul d'òor in le pigne d'un pí. Cheste relazziú i pudaress s’esplicá par la presenza da la Sequenza da Fibonacci in chiist fenòmen, però cheest-chí al è un tema debatüü.
Par altra banda, una bona aprussimazziú da la spirala d’òor sa la pöö truvá in la cjosca dal nautilus u de le lümaghe da maar, però vargott sa l pöö mia esplicá sjentíficameent.



















































































