Numer del Nusselt
El numere del Nusselt Nu a l’è on grupp senza unitaa de misura che l’esprìmm el rappòrt intra el fluss de calor scambiàa per convezion e el fluss de calor scambiaa per conduzion tèrmica. [1]
A se definìss donca inscì:
indoe
- h a l’è el coefficient de convezion;
- a l’è la longhèzza caratteristica (o ben la longhèzza del còrp soggètt a la convezion sforzada);
- a l’è la conduttività tèrmica del fluid.
Calcol del numer del Nusselt in del caso de la convezion sforzada[Modifega | modifica 'l sorgent]
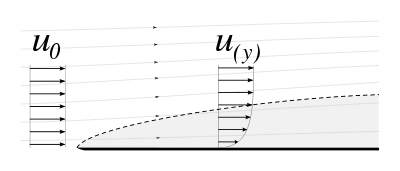
La relazion pussée doprada a l’è chèsta chì:
- che la var per 0,6<Pr<60 e la var per ‘na piastra isotèrma.[3]
indoe el numer del Nusselt l’è correlàa cont el numer del Reynolds e ’l numer del Prandtl, indoe C, m e n hinn di coefficient che varien second la geometria e del tipo de mòto ( regimm laminà e regimm turborent). Per capì se el regìmm l’è laminà o turborent a gh’è de vedè se el numer del Reynolds a l’è sòta o sora el sò valor critic che in del caso de ona piastra piana a l’è Re=500000 con C=0,664, m=1/2, n=1/3 per el moto laminà, C=0,037, m=4/5, n=1/3 per el regìmm turborent. El numer del Reynolds de vèss considerà l’è quèll in corrispondenza de la sezion final de la piastra.
A gh’è anca di casi indoe gh’hinn tutt e du i tipi de mòto de già che ona piastra la po’ vèss nò assée longa de podè trascurà la zòna de mòto laminà e se dopra la relazion: [4]
- che la var per 0,6<Pr<60per 'na piastra isotèrma; quèll valor chì l'è 'na media quand che i lònghèzz indoe el fluss a l'è turborent e laminà hinn pressappòch l'istèss, a l'incontrari gh'è sariss de fà 'na media di Numer del Nusselt pesada in sui du tràtt.
In del caso di geometrij divèrsi se dopera despèss quèsta relazion chì con di alter coefficient oppur di alter relazion ch’hinn semper funzion di numer del Reynolds e del Prandtl.[5]
Calcol del numer del Nusselt in del caso de la convezion natural[Modifega | modifica 'l sorgent]
La relazion pussée doprada a l’è chèsta chì:
indoe
- Gr a l’è el numer del Grashof;
- Pr a l’è el numer del Prandtl;
- Ra a l’è el numer del Rayleigh : ;
- C, n hinn di coefficient che varien second la geometria e del numer del Rayleygh.
In del caso di geometrij divèrsi se dopera despèss quèsta relazion chì con di alter coefficient oppur di alter relazion ch’hinn semper funzion di numer del Grashof e del Prandtl.[7]
Riferiment[Modifega | modifica 'l sorgent]
- ↑ Sandro Longo (2011). Analisi dimensionale e modellistica fisica: principi e applicazioni alle scienze ingegneristiche (in italian). Springer, 219. ISBN 88-470-1871-4.
- ↑ Yunus A. Çengel (2005). Termodinamica e trasmissione del calore (in italian). McGraw-Hill, 373. ISBN 88-386-6203-7.
- ↑ Yunus A. Çengel (2005). Termodinamica e trasmissione del calore (in italian). McGraw-Hill, 379-380. ISBN 88-386-6203-7.
- ↑ Yunus A. Çengel (2005). Termodinamica e trasmissione del calore (in italian). McGraw-Hill, 380. ISBN 88-386-6203-7.
- ↑ Yunus A. Çengel (2005). Termodinamica e trasmissione del calore (in italian). McGraw-Hill, 383-410. ISBN 88-386-6203-7.
- ↑ Yunus A. Çengel (2005). Termodinamica e trasmissione del calore (in italian). McGraw-Hill, 418. ISBN 88-386-6203-7.
- ↑ Yunus A. Çengel (2005). Termodinamica e trasmissione del calore (in italian). McGraw-Hill, 419-430. ISBN 88-386-6203-7.







